|
|
 |
3MeV 이하의 광자(X-선 또는 감마선)에 의해 공기의 단위질량당 생성된 전하의 양으로 정의되며 전통적인 단위는 "뢴트겐(Roentgen, R)"이고 SI단위는 "C/kg"이다.
![]() 1R =
2.58 ×10-4 C/kg
1R =
2.58 ×10-4 C/kg
물질의 단위질량당 흡수된 방사선의 에너지로 정의되며 전통적인 단위는 "라드(Roentgen Absorbed Dose, rad)"이고 SI단위는 "그레이(Gray, Gy)"이다.
![]() 1rad
= 100erg/g
1rad
= 100erg/g
1Gy = 1J/kg = 100rad
조사선량은 광자가
공기에 입사되는 경우에만 적용가능하지만 흡수선량은 모든 종류의
방사선이 인체조직을 포함한 모든 물질에 입사되는 경우에도
적용가능하다.
조사선량 1R은 공기중에서 광자에 의한 흡수선량 0.876rad와 등가하고,
방사선방호 목적, 즉 인체조직에서의 광자에 의한 흡수선량 0.95rad(대략
1rad)와 등가하다.
감마선을 방출하는
점선원으로부터 일정거리에서 조사선량은 쉽게 계산할 수 있다. 즉
선원으로부터 1m 반경을 지닌 구와 2m 반경을 지닌 구를 가정해 보자.
구의 면적은 4![]() r2으로
계산되므로 2m 반경인 구의 면적은 1m 반경의 구보다 22배만큼
넓어진다. 따라서 선원으로부터 거리가 두배가 되면 단위면적당
방사선 준위는 1/4로 줄어들 것이다. 이를 수학적으로 표현하면 "방사선의
강도는 선원으로부터의 거리의 역자승에 비례한다"라고 하며
"역자승 법칙(inverse square law)"이라고 부른다.
r2으로
계산되므로 2m 반경인 구의 면적은 1m 반경의 구보다 22배만큼
넓어진다. 따라서 선원으로부터 거리가 두배가 되면 단위면적당
방사선 준위는 1/4로 줄어들 것이다. 이를 수학적으로 표현하면 "방사선의
강도는 선원으로부터의 거리의 역자승에 비례한다"라고 하며
"역자승 법칙(inverse square law)"이라고 부른다.
실제의 방사선원에서 점선원이란 존재하지 않지만 계산의 편의상
선원의 장축의 길이보다 3배 이상 떨어진 위치에서 선원의
방사선량을 측정할 경우 점선원으로 가정하고 역자승법칙을
적용하더라도 큰 오차없이 조산선량을 다음과 같이 계산할 수 있다.
![]()
![]() : 감마상수(R·m2/Ci·h)
: 감마상수(R·m2/Ci·h)
S : 선원의 방사능(Ci)
d : 선원으로부터 거리(m)
여기서
감마상수는 1Ci의 선원으로부터 1m 거리에서의 조사선량률(R/h)로
정의된다.
만약 선원에서 방출된 감마선의 에너지가 50keV에서 3MeV사이에
있다면 "![]() =0.5E"에
대략적으로근사한다. 이와 같은 관계를 이용한 계산은 ±20%의
오차범위에 있는 결과를 줄 것이다.
=0.5E"에
대략적으로근사한다. 이와 같은 관계를 이용한 계산은 ±20%의
오차범위에 있는 결과를 줄 것이다.
위에서 구한 조사선량으로부터 공기중에서의 흡수선량은 다음의
관계식으로 계산할 수 있다.
Dair = 0.876 × X [cGy]
 또한
방사선방호의 관점에서 공기에서의 조사선량 및 흡수선량 보다는
인체조직에서의 흡수선량을 알 필요가 있다. 이러한 경우에
흡수선량의 측정을 가능하게 하는 것이 "Bragg-Gray
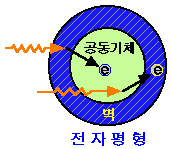
원리"이다. Bragg-Gray 원리란 아래 그림에서 보인 것과 같이
공동벽과 공동기체 사이에 "하전입자 평형" 또는 X-선 또는
감마선에 대해서는 상호작용으로 생성된 2차전자의 "전자평형"
상태가 이루어진다는 가정 아래 "벽물질과 공동기체의
흡수선량비는 질량저지능비와 같다"는 것이다. 아래식에서
벽물질을 인체조직으로할 경우 인체조직에서의 흡수선량을 계산할
수 있다.
또한
방사선방호의 관점에서 공기에서의 조사선량 및 흡수선량 보다는
인체조직에서의 흡수선량을 알 필요가 있다. 이러한 경우에
흡수선량의 측정을 가능하게 하는 것이 "Bragg-Gray
원리"이다. Bragg-Gray 원리란 아래 그림에서 보인 것과 같이
공동벽과 공동기체 사이에 "하전입자 평형" 또는 X-선 또는
감마선에 대해서는 상호작용으로 생성된 2차전자의 "전자평형"
상태가 이루어진다는 가정 아래 "벽물질과 공동기체의
흡수선량비는 질량저지능비와 같다"는 것이다. 아래식에서
벽물질을 인체조직으로할 경우 인체조직에서의 흡수선량을 계산할
수 있다.
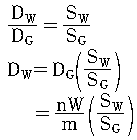
DW와 DG : 벽물질과 공동기체의 흡수선량
SW와 SG : 벽물질과 공동기체에서의 질량저지능
n : 공동내에서 생성된 이온쌍의 수
m : 공동기체의 질량
W : 하나의 이온쌍을 만드는데 필요한 평균에너지